Не будем ходить слишком далеко и сразу возьмем несколько работ из последнего выпуска Российского кардиологического журнала. Что нам интересно в этих статьях? Обычно информация об использованных статистических методах содержится в последнем абзаце раздела «Методы». Там авторы могут сообщить, с помощью каких программ они собирали и обрабатывали данные, какие методы и в каких случаях использовали, какие результаты считали значимыми.

Данные описательной статистики чаще всего можно найти в таблице в начале «Результатов» или в «Методах», где авторы обсуждают характеристики исследуемой популяции. Впрочем, все равно стоит понимать, что без прочтения всей статьи и понимания дизайна исследования судить о корректности статистики в нем — не самая верная тактика.

Чтение начнем со статьи И. Б. Ибрагимовой и соавторов «Влияние торасемида на электрическую нестабильность сердца у пациентов с ишемической митральной регургитацией в постинфарктном периоде». В «статистическом» абзаце авторы сообщают нам, что результаты представлены в виде среднего и стандартной ошибки среднего.

Сначала поговорим о среднем. С одной стороны, у нас нет никакой информации о характере распределения и проверке этого со стороны авторов. Зато размер выборки — 46 и 50 человек — может считаться достаточным, чтобы заочно посчитать распределение нормальным и пользоваться средним.

На будущее запомним, какие статистические критерии использовали авторы — это непараметрические тесты Вилкоксона и Манна — Уитни. Непараметрические тесты применяются в случае «неидеальных» данных, например, при распределении, отличном от нормальной или дискретной переменной. В целом не будет ошибкой применять их и в «идеальных» случаях, но это все же неоптимальный выбор метода, который требует пояснения от авторов, учитывая, что использованная описательная характеристика — среднее.

Теперь про стандартную ошибку среднего. Раньше мы не обсуждали этот параметр, поэтому сначала немного теории. Стандартная ошибка среднего демонстрирует, насколько выборочное среднее (то есть то, которое мы получаем по изучаемым пациентам) отличается от среднего по генеральной совокупности (то есть вообще всех людей, которые могли попасть в нашу выборку). Довольно очевидно, что чем больше наша выборка, тем «точнее» среднее и тем меньше его стандартная ошибка. Собственно, стандартная ошибка вычисляется делением выборочного стандартного отклонения на квадратный корень числа объектов в выборке.

Вообще, в статьях может использоваться стандартная ошибка среднего как показатель разброса данных в выборке. Только в этом есть большая проблема: стандартная ошибка среднего не показывает этого разброса данных. Если мы возьмем ситуацию с очень большой выборкой, то ошибка среднего там будет заведомо очень мала, даже несмотря на то, как реально разбросаны данные в этой выборке. К сожалению, эта характеристика прибавляет ошибке популярности, ведь чем меньше цифра после «±», тем достоверней кажутся результаты. Хотя, конечно, это убеждение далеко от правды.

Кроме того, использование ошибки среднего добавляет путаницы при сравнении нескольких статей. Чтобы понять, почему показатель вариативности одного и того же параметра в схожих группах в двух статьях отличается на порядок, нужно довольно внимательно читать описания статистических методов, понимать разницу между стандартным отклонением и стандартной ошибкой, а также уметь переводить одно в другое.

Так, в статье, с которой мы начали, стандартное отклонение возраста будет равно 2,3 × √46=15,6 лет. Так мы получили цифру, которая в целом довольно близка, например, к полученной в крупном исследовании COMMIT, где также изучались пациенты с острым инфарктом миокарда, и средний возраст ± стандартное отклонение составляли 61,3±11,9 в группе лечения. Учитывая, что в группе там было почти 23 тысячи пациентов, стандартная ошибка среднего составила бы 0,07! Авторы могли бы ошибочно использовать это значение и написать 61,3±0,07, но это совершенно не значило бы, что исследователям удалось набрать 20 тысяч пациентов в возрасте ровно 61 год и 3 месяца с развившимся инфарктом миокарда.

Кроме того, в статье, которую мы читаем, в критериях включения стоит возрастное ограничение: в исследование не включались пациенты старше 70 лет. Удивительно при этом наблюдать такой разброс данных, верхний конец которого (60,1 +15,6) довольно сильно выбивается из установленной границы. Вероятно, такие цифры как раз появились из-за того, что реальное распределение возраста в выборке было довольно далеко от нормального, но вполне возможно, что это и просто случайность при не очень большом размере выборки.

Но давайте двинемся дальше и посмотрим другую статью из того же номера — «Clopidogrel response in acute coronary syndrome patients with CYP2Y12*2 and CYP2Y12*3 polymorphisms» Rahmatini R. et al. В основном нас интересуют пока все те же части текста — абзац «Statistical analysis» и таблицы с описательными характеристиками выборки. В данном случае авторы указали тест, которым они проверяли распределение данных, — Шапиро — Уилка. Результаты самого теста не представлены, но подразумевается, что данные, представленные как среднее и стандартное отклонение, распределены нормально. В таком виде содержатся данные о возрасте пациентов, но, вероятно, из-за типографской, а не статистической ошибки стандартное отклонение в таблицу не попало.

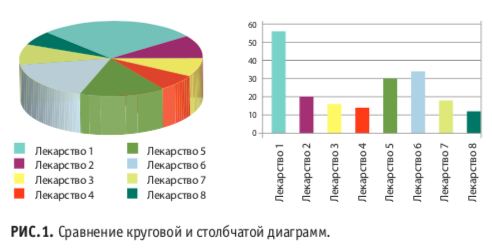
Впрочем, в этой статье можно обратить внимание на другой аспект — рисунок 1, который отражает распределение между «резистентными» к клопидогрелу пациентами и чувствительными к нему. Представлен он в виде круговой диаграммы, или, как его обычно называют, «пирога». Обычно статистики не любят таких графиков, потому что воспринимать площади секторов читателю гораздо сложнее, чем, например, высоту прямоугольников в столбчатой диаграмме. В данном случае это не так сложно из-за наличия только двух секторов, но если их число вырастает, как на нашем рисунке 1, то читать их становится сложно, а применять их уже совершенно нельзя.

Закончим мы нынешний выпуск англоязычной статьей из European Heart Journal «Left atrial function to identify patients with atrial fibrillation at high risk of stroke: new insights from a large registry» Leung M. et al. Вне зависимости от языка интересовать нас будут все те же части статьи — формальное описание статистического анализа и сводные таблицы с данными. В этот раз в формальном описании авторы не сообщают, как проверялась нормальность распределения, но сразу четко разделяют формы представления данных в зависимости от распределения. Все точно то же, о чем мы говорили в наших прошлых публикациях. Соответственно, в таблице мы видим, как применяются оба подхода. Так, например, общий холестерин указан как среднее и стандартное отклонение, а триглицериды — уже как медиана и 25- и 75-процентные квартили.

Вряд ли в этом можно найти какой-то значительный предметный смысл, учитывая, что квартили лежат довольно симметрично, и, не зная реальной формы распределения, скорее это следует считать некоторой случайностью. Однако эти случайности никак нельзя упускать, поскольку при дальнейшем анализе распределение очень важно учитывать для выбора правильных тестов и получения корректных результатов. Мы уже упоминали об этой проблеме в этой публикации, но более подробно начнем знакомиться со статистическими критериями и их практическим значением в следующий раз.