Статьи
Цифры в медицине: «Распределяй и властвуй!»
В предыдущей части нашего рассказа мы измеряли рост сотрудников редакции «Современной кардиологии» и получили гистограмму (рис. 1), которая показывает, сколько человек относится к каждой ростовой группе.
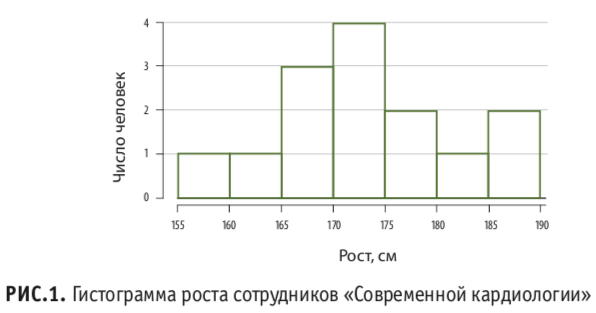
Теперь для начала давайте посчитаем вероятности того, что случайно выбранный сотрудник редакции будет относиться к той или иной ростовой группе. Раз у нас всего 14 сотрудников, и четверо из них ростом от 170 до 175 сантиметров, то наш шанс «попасть» в такого сотрудника 4/14 = 28,6%. Повторим это для каждой группы и нанесем результаты на график. Получившаяся кривая (рис. 2) своими очертаниями, конечно, очень сильно напоминает исходную гистограмму. Но все же она довольно «треугольная» из-за малого числа точек.
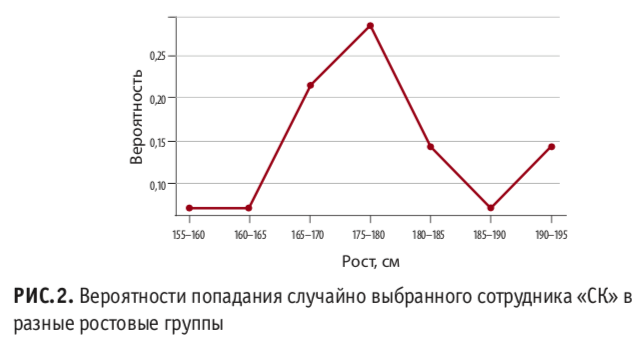
Чтобы увидеть более широкую картину, давайте используем для построения графика, например, показатели систолического давления (САД) у 500 случайных человек. Проделаем для них все те же операции: построим гистограмму и посчитаем вероятности для каждой группы.
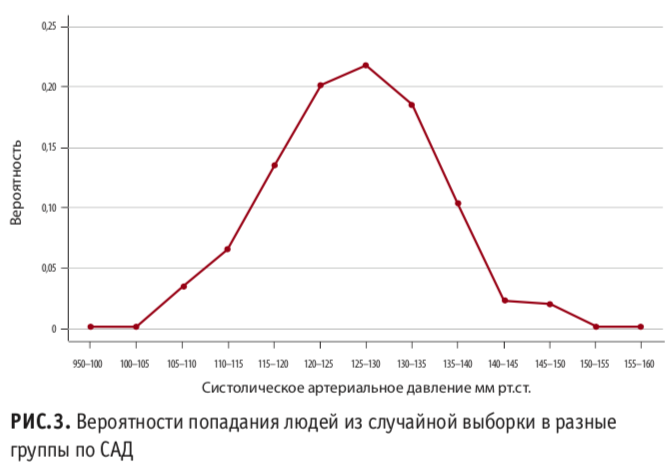
В этот раз мы получили более плавную кривую (рис.3), но у нее все еще есть недостаток. При переходе к гистограмме мы сгруппировали нашу непрерывную переменную, артериальное давление (вы же помните, почему АД — непрерывная переменная? Это обсуждалось в первой части нашего рассказа), на отдельные дискретные группы. Из-за этого мы потеряли возможность с помощью этого графика оценить, какая вероятность получить у случайного человека САД ровно 127 мм рт. ст. Мы знаем только о том, что его вероятность попасть в группу 125–130 мм рт. ст. равна примерно 22%.
И вот как раз для этой цели предназначены описания вероятностей отдельных событий, и нам необходимо ввести понятие распределения, которое описывает область возможных значений какого-то события (измерения АД случайного человека) и вероятности его исхода (собственно, значения АД). Мы не будем вдаваться в математический аппарат, позволяющий нам сформулировать или хотя предположить распределение для каждой случайной выборки, но можем использовать современные компьютеры и программы и нарисовать его график, изображенный на рис. 4. синим цветом.
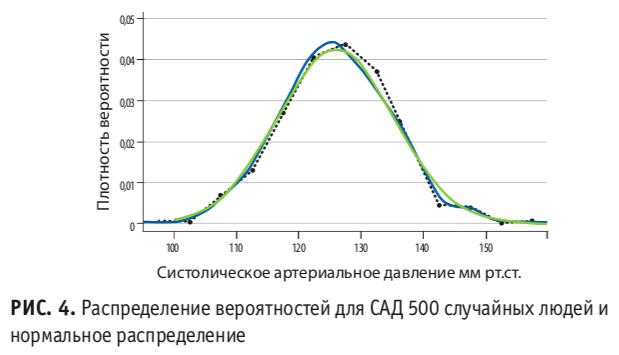
Обратите внимание на несколько деталей. Во-первых, черная кривая — это копия нашего графика 3, но заметно уменьшенная по вертикальной оси. Сделать это пришлось, чтобы получились сравнимые масштабы. В «натуральную величину» черный график очевидно сильно выше, ведь и вероятность попасть в довольно большой промежуток 120–125 мм рт.ст. заметно больше, чем в отдельную точку на графике. Но важнее здесь то, насколько схожи очертания этих двух кривых. Это неплохое доказательство того, что гистограмма достаточно корректно описывает получившееся распределение.
Второй момент уже гораздо более «математический» и связан с размерностью вертикальной оси — плотностью вероятности. Все дело в том, что, строго говоря, абсолютная вероятность попасть в конкретное значение непрерывной величины практически равна нулю. Происходит это из-за того, что шкала непрерывной величины содержит бесконечное множество значений: 125,5 мм рт.ст.,
125,501 мм рт.ст., 125,5000003 мм рт.ст. и так далее. В реальной жизни эта разница не слишком заметна из-за ограниченной точности измерений, а вот математикам приходится оперировать именно плотностью вероятностей. Но оставим это им и попытаемся понять, зачем же мы вообще будем использовать распределение.
А для этого нам потребуется третья, зеленая кривая с рис. 4. Надеемся, многие узнали в нем нормальное, или Гауссово, распределение. Чем же оно так примечательно? Во-первых, нормальное распределение очень часто встречается в реальной жизни. По нему зачастую распределяются случайные величины, зависящие от многих независимых факторов, как, например, систолическое давление из нашего примера, или вес, или число листьев на случайном дереве.
Из этого следует и вторая особенность нормального распределения — в статистике оно давно и хорошо известно. Его особенности и применения изучаются уже несколькими поколениями математиков, и на основе его свойств построены многочисленные статистические тесты, ставшие «классикой жанра»: дисперсионный анализ, тест Стьюдента и многие другие. О них мы еще обязательно поговорим.
И третий момент: форма кривой нормального распределения полностью определяется только средним значением параметра и его среднеквадратичным отклонением. То есть, зная эти два показателя и будучи уверенными, что наша выборка распределена нормально, мы можем однозначно и точно эту выборку описать.
Вспомним теперь, что весь этот разговор мы начали с целью понять, когда же стоит использовать для описания выборки среднее и среднеквадратичное отклонение, а когда — медиану и квартили. Вот и наш ответ: если распределение в выборке нормальное или, по крайней мере, близко к нормальному, то оптимальный способ ее описать — это среднее и стандартное отклонение. В противном случае следует выбирать медиану и квартили или другие, более редкие способы, опираясь на характеристики распределения.
Последнее, что осталось понять, — а как, собственно, определить, что распределение близко к нормальному? Самый простой способ мы можем попробовать прямо на рис. 4 — это визуальное сопоставление гистограммы или плотности вероятностей с формой нормального распределения. В нашем примере очевидно, что они очень похожи, и мы вполне можем использовать среднее. Кроме того, существует график квантилей, упрощающий такое визуальное сравнение, но его мы оставим для самостоятельного изучения читателям.
Визуального сравнения зачастую вполне достаточно, особенно если данных много и никакие редкие события, например, очень высокий человек, попавший в выборку, не портят картину. Но, конечно, есть и более формальные тесты, позволяющие объективно определить, с какой вероятностью выборка отличается от нормального распределения. Например, тест Шапиро — Уилкса или тест Колмогорова — Смирнова в модификации Лиллиефорса и некоторые другие. И о них мы тоже обязательно поговорим. А пока давайте подводить итоги.
В идеальной ситуации научная статья с описательной статистикой должна содержать указание на то, как проверялась нормальность распределения параметров в данной выборке. В реальности этот момент достаточно часто опускается авторами. Иногда — осознано. Например, если параметр «простой», такой как возраст пациентов в группе, а число пациентов достаточно велико — сотни и более. Или же читателю остается доверять авторам в вопросе корректности выбора той или иной метрики, предполагая, что среднее и среднеквадратичное отклонение было использовано уже после проверки распределения на нормальность и результат ее был подходящим для такого выбора. Медиана же остается более универсальным, хотя и несколько более сложным для понимания выбором, который меньше зависит от свойств распределения.

















